Categoría: bachillerato
-
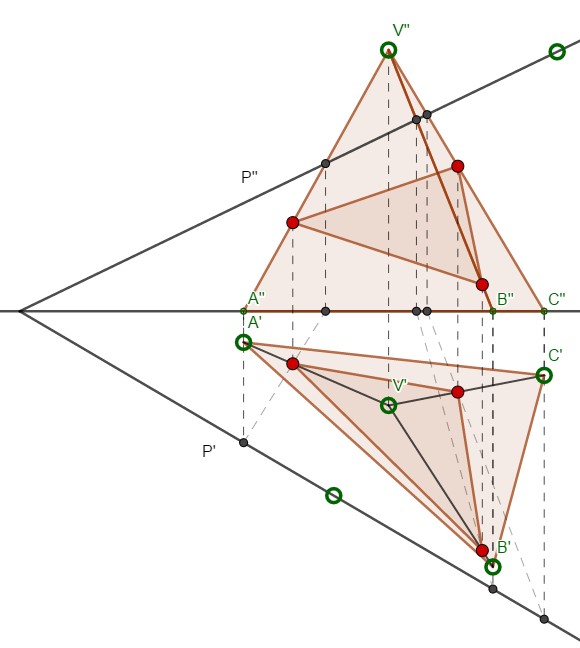
Intersección pirámide con plano oblicuo – Sistema diédrico
este es uno de los ejercicios de enlaces mas común
-
integración por partes
este es un ejemplo sencillo de como integrar por partes recuerda: «un día ví una vaca vestida de uniforme»
-
sistema completo de sucesos
un conjunto de sucesos es completo cuando:
-
propiedades de una probabilidad
1.- la probabilidad del suceso imposible es 0: 2.- para un suceso complementario se cumple: 3.- para la unión de dos sucesos se tiene: que tambien podemos escribir:
-
tangencias – la cuchara
este es uno de los ejercicios de enlaces mas común
-
integrales inmediatas
hay una serie de integrales directas que debemos saber, a partir de ellas obtendremos otras mas complicadas
-
la k de la integral indefinida
siempre que realicemos una integral indefinida, tendremos que añadir una constante al resultado. ¿por qué?
-
otro ejemplo de integral
como la integral es la inversa de la derivada, si: entonces:
-
¿que es una integral?
la integral es la inversa de la derivada
